Виды механических волн, Механические волны, теория и онлайн калькуляторы

Скорость продольной волны в твердом теле и упругих волн в жидкостях ,. Процесс распространения колебаний в среде называется волной. Если наблюдать за любой точкой шнура, мы увидим, что каждая точка совершает колебания с тем же периодом Т. Амплитуда скорости груза. Механика вращательного и колебательного движения Вид работы: Тест Выполнена: 30 ноября г.
Монохроматическая волна в струне описывается выражением:.

Уравнение 1 называют уравнением бегущей волны. Все элементы струны, если по ней проходит монохроматическая волна выполняют гармонические колебания с одинаковыми частотами и амплитудами, но разными фазами. Рассмотрим струну целиком в один момент времени зафиксируем время в выражении 1. На этой картине можно увидеть фиксированную косинусоиду.
Длина волны равна расстоянию распространения определенной фазы колебаний за один период. При детальном рассмотрении волн, очевидно, что колебания осуществляют не только частицы вдоль одной оси, происходят колебания совокупности частиц, которые находятся в некотором объеме. Волна при ее распространении охватывает новые области пространства.
Волновой поверхностью считают геометрическое место точек, совершающих колебания в одной фазе. Волновых поверхностей бесконечное множество. Волновой фронт - это тоже волновая поверхность, единственная в каждый момент времени. Волновые поверхности имеют любые формы.
В самом простом случае - это система параллельных плоскостей иди концентрических сфер. Волна называется плоской, если ее волновые поверхности представляют собой совокупность параллельных плоскостей. Уравнение 1 является уравнением плоской бегущей волны. Если плоская волна будет распространяться в противоположном направлении, то ее уравнение:.
В общем случае при распространении волны по оси Z в веществе, которое не поглощает энергию можно записать как:. Используя его уравнение 5 записывают в виде:. Волна называется сферической, если ее волновые поверхности - это система концентрических сфер. Уравнение сферической волны:. При распространении сферической волны, даже если среда энергию не поглощает, то амплитуда волны убывает обратно пропорционально расстоянию от центра волны. Отметим, что уравнение 7 выполняется, только если расстояние от источника волн до точки рассмотрения, существенно больше, чем его размеры то есть, если источник можно считать точечным.
Решением уравнения 8 является уравнение любой волны, то есть ему удовлетворяют уравнения и 6 , и 7. Какова максимальная скорость частиц среды в которой распространяется эта волна? Волну будем считать плоской, считаем, что она распространяется по оси X, волновое уравнение запишем как:. Если мы бросим камень в воду, то вокруг места падения камня «пойдёт круги».
Эти круги — тоже волны. Источниками волн являются колебания. Колеблются стебли растений, деформируемые ветром, колеблются частицы воды, колеблется конец шнура.
А колебания, возникшие в одном месте, передаются другим частицам. То, что мы называем волной, и есть распространение колебаний от точки к точке, от частицы к частице.
Моделью образования волны в шнуре может служить цепочка шариков, имеющих массу, между которыми действует сила упругости. Вообразим, что между шариками расположены маленькие пружинки. Пусть шарик 1 отведен вверх и отпущен. Пружинка, связывающая его с шариком 2, при этом растянется, возникнет сила упругости, которая действует не только на шарик 1, но и на шарик 2. Скорость волны зависит от упругих свойств а также плотности среды. Поскольку скорость распространения волны зависит от свойств среды, длина волны при переходе волны из одной среды в другую изменяется, хотя частота колебаний остается неизменной.
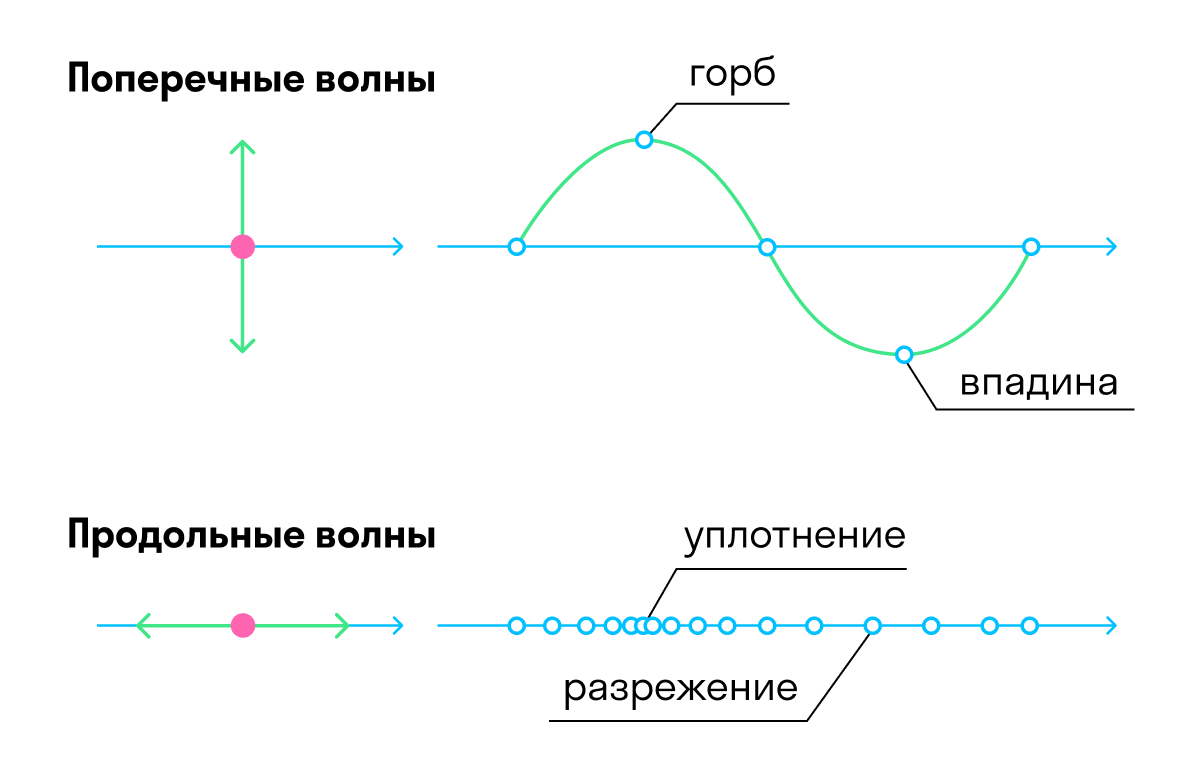
Так же как и колебания, волны делятся на простые гармонические и сложные. Колебания, возбуждаемые в одной точке, в однородной изотропной среде распространяются от нее равномерно по всем направлениям, такая волна называется сферической.
Если источник колебаний имеет значительную плоскую поверхность, то волна от него будет распространяться направленным потоком перпендикулярно поверхности источника; такая волна называется плоской.
Составим уравнение плоской гармонической волны, позволяющее определить смещение S точки Б среды, находящейся на любом расстоянии x от начальной точки А , в направлении распространения волны в любой момент времени. Тогда для точки Б уравнение колебания будет:. График этой зависимости как бы моментальный снимок волны называют графиком волны. Для простой гармонической волны график имеет форму синусоиды или косинусоиды. Зависимость между смещением S точки, ее координатой x и временем t , выраженная в дифференциальной форме называется волновым уравнением.
Для составления уравнения плоской волны находим частные производные второго порядка от смещения S по времени t и координате x :. Таким образом, вторая производная смещения по времени пропорциональна второй производной смещения по координате. Коэффициент пропорциональности равен квадрату скорости распространения волны V. Это и есть дифференциальное уравнение плоской волны, распространяющейся в направлении оси x со скоростью V см.
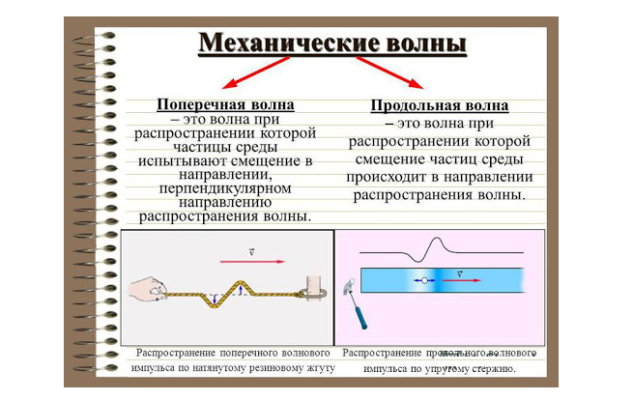
Оно в наиболее общем виде описывает распространение волнового процесса. Основные характеристики амплитуда, период или частота, длина волны и форма колебаний продольной волны, её уравнение и графику аналогичны поперечной. При волновом движении происходит перенос энергии, которая состоит из кинетической и потенциальной энергий колеблющихся частиц среды. Причем потенциальная энергия обусловлена деформацией вещества при взаимном смещении частиц.
В отличие от колебаний свободного тела в волне не происходит взаимного перехода кинетической и потенциальной энергии частиц. Мгновенные значения той и другой энергии изменяются одновременно в фазе соответственно изменению смещения частиц. Из формулы 1.
Величина, численно равная средней энергии Е ср , переносимой волной в единицу времени t через заданную поверхность S , перпендикулярную направлению распространения волны, называется потоком энергии через эту поверхность:. Поток энергии, приходящийся на единицу поверхности, называется плотностью потока энергии :. Плотность потока энергии называют также интенсивностью волны. Плотность потока энергии, переносимого волной, можно рассматривать как вектор, совпадающий по направлению с вектором скорости волны.
Вектор , показывающий направление распространения волны и равный потоку энергии, проходящему через единичную площадку, перпендикулярную этому направлению, называют вектором Умова:. Вектор Умова для упругой волны зависит от плотности среды, квадрата амплитуды колебания частиц, квадрата частоты колебаний и скорости распространения волны. Николай Алексеевич Умов является исследователем потока энергии.
Идеи о движении энергии были изложены в его диссертации "Уравнения движения энергии в телах", защищенной им в году на физико-математическом факультете Московского университета. И только через десять лет к таким же выводам о движении энергии пришел английский физик Пойнтинг. Имя Умова вошло в историю физики.
Файловый архив студентов.
Логин: Пароль: Забыли пароль? Email: Email повторно: Логин: Пароль: Принимаю пользовательское соглашение. FAQ Обратная связь Вопросы и предложения.