Непозиционная система счисления примеры, Информатика

Детские сады и ясли Школы, гимназии, лицеи Среднее профессиональное образование ссузы Высшее образование вузы Образование за рубежом Законодательство в образовании Научно-методический раздел, библиотеки Профориентация ЕГЭ, ГИА и подготовка к поступлению Олимпиады Дополнительное образование для самых маленьких Дополнительное образование для школьников Магистратура,аспирантура, доп. В связи с соотношением достоинств к недостаткам данных систем они были почти полностью вытесненными более совершенными позиционными исчислениями. Рынок ИТ-услуг в России: оценки, тренды, крупнейшие участники.
Принцип разделения числового пространства на группы по 60 единиц используется и в настоящее время для определения временных отрезков. Один час состоит из 60 минут, одна минута — из 60 секунд. Вавилонская система представляет собой комбинированный вариант системы счисления, так как представление чисел от 1 до 60 подчинено непозиционному принципу, а числа свыше шестидесяти представляются с использованием позиционного подхода.
Например, число 34 в вавилонской системе записывается как последовательность из трех горизонтальных клиньев, за которыми следует четыре прямых клина. А число 84 будет начинаться с прямого клина, обозначающего 60, за которым следуют два лежащих клина и затем четыре прямых. Для обозначения чисел в различных бытовых ситуациях Майя использовали непозиционную систему представления чисел, в которой записывались числа от 0 до 19 с помощью знаков, представляющих собой комбинации точек и горизонтально расположенных отрезков.
Например, цифра для обозначения числа 17 выглядит как две точки, расположенные над тремя горизонтальными черточками.

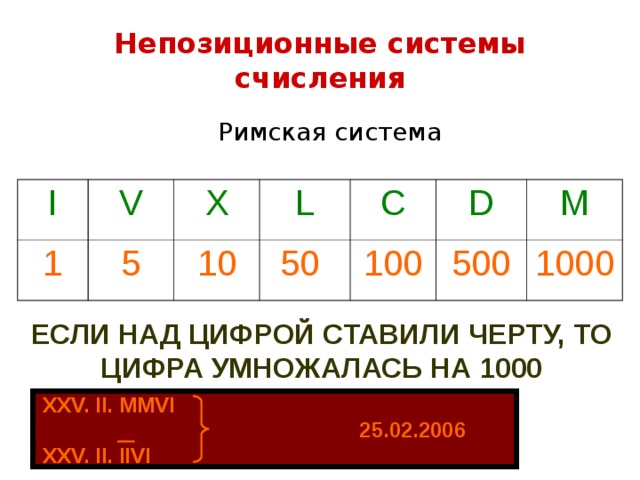
Для представления чисел используются позиционные и непозиционные системы счисления. В непозиционных системах расположение знаков, составляющих числа не влияет на их числовые значения. Самой известной непозиционной системой является система римских цифр. Известные исторической науке системы записи чисел древних народов Египта, Вавилона, цивилизации Майя применяли непозиционный принцип представления чисел, используя различные знаки для обозначения числовых эквивалентов.
Непозиционная система счисления. Средняя оценка: 4. Что мы узнали? Основание системы счисления равно двум. Изменение положения символа в числе не влияет на его числовое значение.
Если цифру в числе переместить из одного разряда в другой, ее количественное значение измениться.

Выполнять умножение и сложение чисел в системе счисления можно поразрядно, записывая их столбиком, друг под другом. Сейчас в математике используются две непозиционные системы счисления — биномиальная система счисления и система остаточных классов. В обеих из них всё зависит от алгоритмов расчёта, и если понимать их отличие от позиционных систем, то работать с ними становится гораздо проще.
Биномиальная система счисления — это когда число представляется в виде суммы биноминальных коэффициентов. Слово «биномиальный» означает, что система основана на биноме Ньютона — способе разложения одних чисел на другие.
Эта система счисления используется в комбинаторике — с её помощью можно быстро вычислить нужную комбинацию без перебора всех вариантов, которые идут перед ней. А ещё по этому же принципу производят тестирование ПО, контроль качества и анализ проведённой лотереи — находят такие комбинации и сочетания факторов, которые вероятнее всего могли привести к каким-то важным результатам.
Система остаточных классов основана на модулярной арифметике, когда числа сравниваются по модулю дают ли при делении один и тот же остаток.
Там всё состоит из базисов, модулей и похоже на работу с матрицами. Благодаря тому свойству, что некоторые вычисления имеют только одно решение, система остаточных классов используется в информационной безопасности, контроле за ошибками и для обеспечения надёжности космической или военной техники. В следующей статье мы разберём хитрую задачку из собеседования, связанную как раз с римской системой счисления. Такое любят спрашивать при устройстве в разные крупные компании, чтобы оценить кругозор будущего сотрудника.
Спрашиваем практикующего iOS-разработчика, как попасть в эту отрасль и начать делать приложения в App Store. Разбираем на примере римской системы.

Берём самое большое римское число и смотрим, наше число больше или нет. Если наше больше — вычитаем из нашего римское и записываем его. Если не больше — переходим к следующему римскому. Так делаем до тех пор, пока у нас в остатке не получится ноль. Наше больше, поэтому отнимаем и добавляем новую букву: M. Остаток — Снова проверяем с самым большим числом — M. Наше число меньше, поэтому берём следующее: CM Запоминаем остаток и добавляем CM к нашему числу: MCM Берём остаток — 98 — и проверяем снова все римские числа сверху вниз.
Чтобы записать число, римляне использовали не только сложение, но и вычитание. Правила составления чисел в римской системе счисления:.
В старину на Руси широко применялись системы счисления, напоминающие римскую. Они назывались ясачные.
С их помощью сборщики податей заполняли квитанции об уплате подати ясака и делали записи в податной тетради. Добавлять комментарии могут только зарегистрированные пользователи. Главная » Статьи » Системы счисления » Непозиционные системы счисления. Непозиционные системы счисления Люди научились считать очень давно.
Примерно в третьем тысячелетии до нашей эры египтяне придумали свою числовую систему, в которой для обозначения ключевых чисел использовались специальные значки — иероглифы. Каждый такой иероглиф мог повторяться не более 9 раз.